基于顶点纹理的无限大海水仿真
最近手上有了一块7800的显卡,因此就想利用这块强大的显卡做点东西出来。基于顶点纹理的无限大面积海水的算法在脑子想了很久了,但一直苦于没有支持顶点纹理的显卡而无法实现。
拿到显卡以后,就开始三下五除二的写程序。下面是最终的效果图。
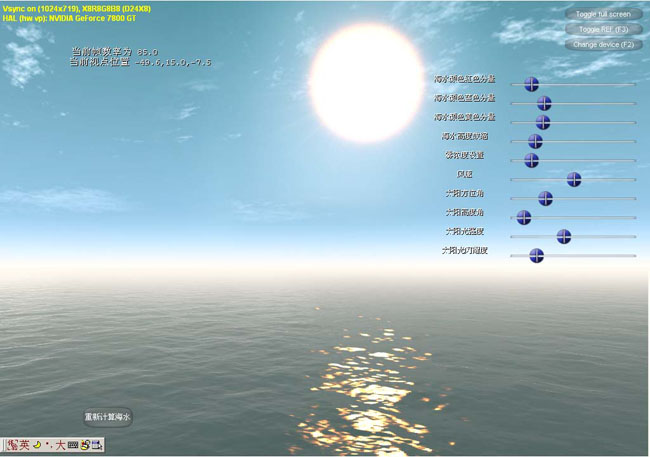
效果图1
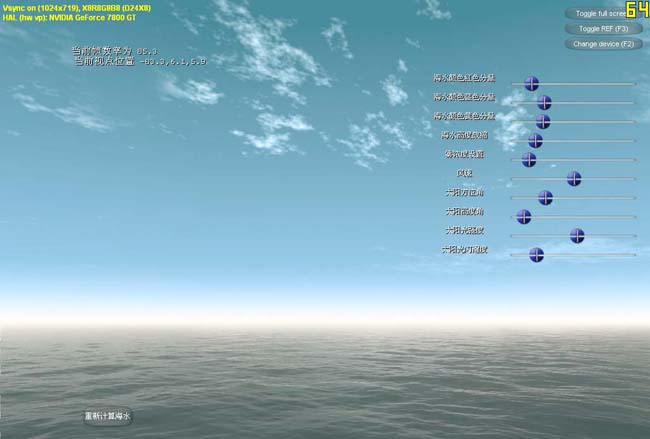
效果图2
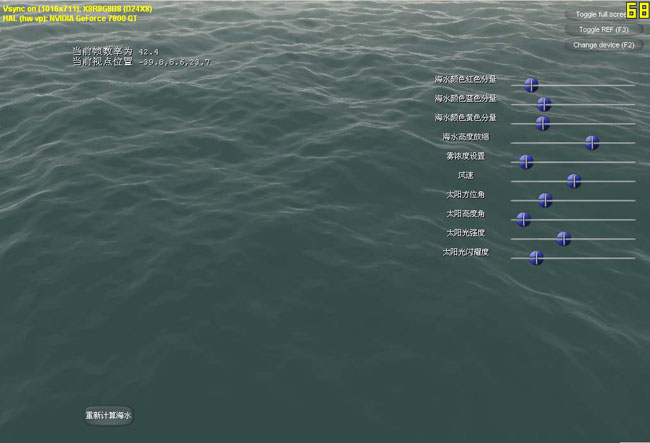
效果图3
主要的方法是,使用一个与视相关的自适应网格(1),使用tessendorf的基于2DFFT的海水仿真算法(2)生成动态的海水高度场,并将高度场存入到顶点纹理当中,然后在顶点着色器中通过取顶点纹理的值对自适应网格进行扰动,形成动态的海水效果。
这个思路虽然简单,但是在目前的显卡中,不支持浮点纹理的双线性滤波,只支持最近点采样的方式,如果使用最近点采样的方式你会发现整个波动效果会有很明显的块状效果(非常讨厌),因此,必须通过shader自己来写一个双线性滤波的函数,另外在我这个算法中还要求根据高度场计算出法线场,由于取顶点纹理是一个非常耗时的操作,如果把这些计算都放在顶点着色器里面进行的话,顶点着色器会成为整个绘制过程的一个大瓶颈。
最终我采用的是多次绘制的方法。首先在一个PS里面进行高度场的滤波,并且计算对应的法线,并且把这个结果渲染到一张浮点纹理中(在PS中做这些操作要比在VS中做这些操作要快很多),然后再利用这张经过滤波处理和法线预计算的浮点纹理作为顶点着色器中的高度场和法线纹理进行高度扰动,以及取法线。
另外。在光照处理方面,海水着色方面参考了(3)。
于是就有了以上的渲染效果图。
最后,我还是要打击一下自己,下面这张是用3dmax加dreamscape插件渲染的海水效果图。看来效果差距还是有的。当然我可以用1/65秒渲染一帧,而它却需要65秒来渲染一帧。

3dsmax海水效果图
(1)http://www-evasion.imag.fr/Publications/2002/HNC02/wavesSCA.pdf
这是法国人写的论文,这个网格构造的思路确实巧妙,值得去研究下。
(2)Simulating Ocean Water, Jerry Tessendorf
这个经典的海水仿真算法我就不解释了,不过这里面最近更新了一个交互海水的算法,也是很值得研究。
(3)http://graphics.cs.lth.se/theses/projects/projgrid/
一个英国人的硕士论文,用到了投影网格概念,不过他的水面效果是使用perlin noise生成#p#page_title#e#


波长为空间周期的n分之一
 (6)
(6) (7)
(7) (8)
(8) (9)
(9)

前提条件和一维时候的情况基本相同:
b:使用多个Gestner-Wave的叠加来合成出整个波动效果。

(15)
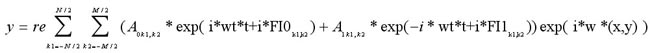
(16)
在后面的章节里,将要介绍使用海洋统计学频谱结合上述使用傅立叶变换描述的海水波动计算公式来进行海水模拟









